| HOME PAGE |
| Spike Density Estimation |
| - Histogram Method |
| - Kernel Method |
| Share it with your friend |
| Tweet |
本節では, 定常ポアソン過程の拡張として, 図
リスケールされた時間軸![]() 上で平均
上で平均![]() の標準指数分布に従う定常ポアソン過程を考え, 実時間へ写像したスパイク時系列が非定常ポアソン過程である.
の標準指数分布に従う定常ポアソン過程を考え, 実時間へ写像したスパイク時系列が非定常ポアソン過程である.
![]() 軸上のイベント系列を
軸上のイベント系列を
![]() とすると, イベント間隔
とすると, イベント間隔
![]() が標準指数分布
が標準指数分布
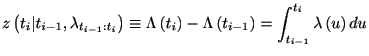
![]() ならば
ならば
![]() へ.
へ.
アルゴリズムの第3ステップで指数分布に従う乱数を発生させるには次に説明する逆関数法を用いる.
変動ポアソン過程において時刻![]() でスパイクが生じた下で, 次のスパイク時刻
でスパイクが生じた下で, 次のスパイク時刻![]() の条件付スパイク密度分布(ISI分布)を求めてみよう:
の条件付スパイク密度分布(ISI分布)を求めてみよう:
![]() ならば
ならば
![]() へ.
へ.
条件付きスパイク密度分布2.2は.
![]() と見れば定常リニューアル過程におけるスパイク密度分布の定義と同義である. 定常リニューアル過程のスパイク密度分布とハザード関数との間には, 1.16のような関係があるから,
2.2と
と見れば定常リニューアル過程におけるスパイク密度分布の定義と同義である. 定常リニューアル過程のスパイク密度分布とハザード関数との間には, 1.16のような関係があるから,
2.2と![]() を見比べて
を見比べて
次に瞬間スパイク生成率(ハザード関数)
![]() を用いる方法が考えれる.
時間を十分小さな幅
を用いる方法が考えれる.
時間を十分小さな幅![]() の区間に区切って, スパイクの発生をベルヌーイ過程で近似する. 各区間で一様乱数を生成し, スパイクの
の区間に区切って, スパイクの発生をベルヌーイ過程で近似する. 各区間で一様乱数を生成し, スパイクの
![]() 確率で発生させる. スパイクが生じない確率は
確率で発生させる. スパイクが生じない確率は
![]() である. 非定常ポアソン過程は履歴を考慮せず微小区間毎に独立に計算できる. 十分小さな
である. 非定常ポアソン過程は履歴を考慮せず微小区間毎に独立に計算できる. 十分小さな![]() を用いればポアソン過程・リニューアル過程を近似することができるはずである.
を用いればポアソン過程・リニューアル過程を近似することができるはずである.
![]() ならば
ならば
![]() .
.
![]() ならば
ならば ![]() へ.
へ.
この直接的な方法はもっとも実装が簡潔だが, 乱数を![]() 回発生させる必要があり計算効率は著しく悪い. 毎回乱数を生成させるよりは,
指数分布に従う乱数を一回発生させ,
その値になるまで
回発生させる必要があり計算効率は著しく悪い. 毎回乱数を生成させるよりは,
指数分布に従う乱数を一回発生させ,
その値になるまで
![]() を数値的に足し込んでいく(積分する)アルゴリズムの方が効率がよい. ただし, この方法も微小区間に区切った関数の数値積分が必要になってくる. それでは次に, 簡潔でかつ効率のよい数値計算法としてよく用いられる希薄化による手法を紹介しよう.
を数値的に足し込んでいく(積分する)アルゴリズムの方が効率がよい. ただし, この方法も微小区間に区切った関数の数値積分が必要になってくる. それでは次に, 簡潔でかつ効率のよい数値計算法としてよく用いられる希薄化による手法を紹介しよう.
希薄化(Thinning[Ogata, 1981,Daley and Vere-Jones, 1988,Heyman and Sobel, 1990])と呼ばれる方法は積分操作を必要としないため, 計算時間が短くて済む場合がある.
まず![]() の範囲にレートが
の範囲にレートが![]() の定常ポアソン過程を生成する.
ただし,
の定常ポアソン過程を生成する.
ただし, ![]() はどの時刻の変動レートよりも大きい値とする(つまり
はどの時刻の変動レートよりも大きい値とする(つまり
![]() に対して
に対して
![]() ). 生成されたスパイク時系列を
). 生成されたスパイク時系列を
![]() .
時刻
.
時刻![]() におけるスパイクは, 規格化した変動レート
におけるスパイクは, 規格化した変動レート
![]() の確率で残す.
残ったスパイク時系列
の確率で残す.
残ったスパイク時系列
![]() は変動レート
は変動レート
![]() のポアソン過程に従う.
のポアソン過程に従う.
![]() ならば
ならば
![]()
![]()