




Next: 定常スパイク時系列の実現
Up: 定常スパイク時系列モデル
Previous: 定常ポアソン過程
Contents
Index
Subsections
前章では記憶なしの特徴をもつスパイク時系列, すなわちポアソン過程について調べた. ポアソン過程のスパイク間隔は指数分布になり, 一定時間内のスパイク数はポアソン分布に従うことをみた. また瞬間スパイク生成率を導入して, (定常)ポアソン過程を定義することもできた.
本章では, スパイクに記憶がある場合のモデルを導入する.
特に大事なのは, スパイク生成率が直前のスパイク生成時刻だけに依存する場合である. この過程はリニューアル過程と呼ばれる.
瞬間生成率が2つ以上前のスパイク生成時刻に依存する一般的なモデルに対して, 直前のスパイクのみに依存することからこの名称で呼ばれる. 一つより前のスパイクについては忘れて,
気分を新たに次のスパイク生成に臨むといったところである.
神経スパイクについては, 強いリニューアル性があることが知られている.
これは神経細胞のスパイク生成機構の生理学上の制約による. 特にスパイク生成後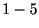 [ms]の間は次のスパイクを生成できない状態になる. これを絶対不応期(Absolute refractory period)と呼び, 神経細胞のリニューアル性の主要な要因である.
この他にも膜上の電位依存性イオンチャネルの非線形効果により, 一度スパイクが生じると複数回のスパイク生成が続くバースト発火という現象などがある. こうした性質を表現するためには, リニューアル過程の活用が欠かせない.
[ms]の間は次のスパイクを生成できない状態になる. これを絶対不応期(Absolute refractory period)と呼び, 神経細胞のリニューアル性の主要な要因である.
この他にも膜上の電位依存性イオンチャネルの非線形効果により, 一度スパイクが生じると複数回のスパイク生成が続くバースト発火という現象などがある. こうした性質を表現するためには, リニューアル過程の活用が欠かせない.
ここで本章で使う統計量をまとめておく. 用語は基本的に生存時間解析(Survival
analysis)に従うが, 生存時間解析ではイベントが固体の死亡を意味するため, 関連語句がスパイクの解析にはなじまない.
そこでいくつかは違う名称で呼ぶこともある. まず, スパイク発生時刻の確率密度分布(probability density function,
p.d.f.)を
とする. これをスパイク密度分布(spike density funtion), もしくはスパイク間隔分布と呼ぶ Inter-spike Interval
(ISI) distribution)と呼ぶ. スパイクの発生時刻が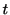 以上である確率を生存関数(survival function)と呼び
以上である確率を生存関数(survival function)と呼び
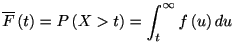 |
(1.8) |
と表す. 生存関数と相補関係にある累積分布関数(cumulative distribution function,
c.d.f.)
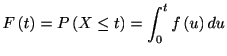 |
(1.9) |
は生存時間分布(lifetime distribution
function)と呼ばれる. スパイク密度分布と分布関数は
の関係にある. ただし記号プライムは微分の意味.
リニューアル過程では瞬間スパイク生成率は, 最後のスパイクの時刻を基準にして時間的に変動する. 少なくとも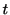 秒間スパイクが生成されず,
秒間スパイクが生成されず, 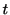 においてスパイクを生成する確率として, 瞬間スパイク生成率
においてスパイクを生成する確率として, 瞬間スパイク生成率
を導入しよう. 生存時間解析(Survival analysiss)では,
ハザード関数(hazard function), 年齢別故障率(age-specific failure rate),
回復関数(recovery function)などの名称で呼ばれる[Cox, 1962].
また, 一般点過程理論では条件付強度関数(conditional intensity function)という.
従ってハザード関数はスパイク密度分布(ISI分布)を用いて次のようにかける.
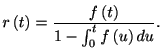 |
(1.13) |
生存関数で表記すると
両辺を0から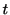 まで積分して, 生存関数とハザード関数の関係式
まで積分して, 生存関数とハザード関数の関係式
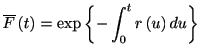 |
(1.14) |
を得る. これから分布関数は
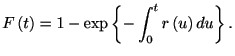 |
(1.15) |
微分すると, スパイク密度分布(ISI分布)は
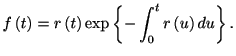 |
(1.16) |
この式は, 確率密度分布とハザード関数の関係式1.13の逆関数になっている.
1.13と1.16は併せて非常に重要な公式なので覚えておこう. 定常ポアソン過程のスパイク密度分が指数分布であることから, 定常ポアソン過程のハザード関数は
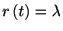 であることがわかる.
であることがわかる.
それでは, 代表的なスパイク密度分布(スパイク間隔分布,
ISI分布)を見てみよう.
ガンマ分布
ガンマ分布は, アーラン分布の拡張であることは既に述べた. リニューアル過程の中でも, 数学的な取り扱いが比較的容易で, 使い勝手が良い分布である.ガンマ分布のハザード関数を求めてみよう.
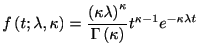 |
(1.17) |
ガンマ分布の平均は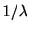 , 分散は
, 分散は
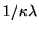 , また
, また
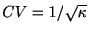 . ただし, 平均が
. ただし, 平均が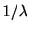 になるように1.5を規格化してある. 図にいくつかの
になるように1.5を規格化してある. 図にいくつかの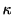 について分布を表示した. ガンマ分布のハザード関数は
について分布を表示した. ガンマ分布のハザード関数は
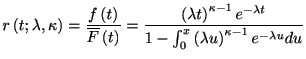 |
(1.18) |
単調に増加する. つまり時間が経につれて, スパイク発生の確率は高まっていく. 十分大きな値でハザード関数は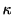 によらず
によらず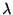 に収束する. すなわち, 十分時間が経つとポアソン過程に近づいていく.
に収束する. すなわち, 十分時間が経つとポアソン過程に近づいていく.
問題 7
ガンマ分布のハザード関数の最大値が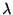 であることを示せ. ハザード関数が単調増加関数であることを示し, 十分大きな
であることを示せ. ハザード関数が単調増加関数であることを示し, 十分大きな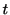 で
で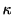 によらず
によらず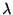 に収束することを示せばよい.
ロピタルの定理を用いよ.
に収束することを示せばよい.
ロピタルの定理を用いよ.
Figure 1.3:
ガンマ密度分布
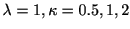
Figure 1.4:
ガンマ分布のハザード関数
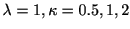
![\includegraphics[width=1\columnwidth]{graphics/book__2.eps}](img161.gif)
![\includegraphics[width=1\columnwidth]{graphics/book__3.eps}](img162.gif) |
ワイブル分布
ガンマ分布のハザード関数が定数に収束するのに対し,
工業製品の故障率のようなイベントの場合は, 経年劣化するからハザード関数は時間とともに増加すると考えられる. 時間とともにハザード関数がべき的に増加する場合を考えよう.
ただし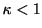 のときはハザード関数が減少関数になる. これは時間が経つにつれてスパイク発生率は低くなることを表す. べき乗のハザード関数を持つ分布はワイブル分布(Weibull distribution)とよばれ
で与えられる. この表記では, 期待値は
のときはハザード関数が減少関数になる. これは時間が経つにつれてスパイク発生率は低くなることを表す. べき乗のハザード関数を持つ分布はワイブル分布(Weibull distribution)とよばれ
で与えられる. この表記では, 期待値は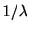 ,
分散は
,
分散は
![$ 1/\lambda^{2}\left[ \Gamma\left( 1+2/\kappa\right)
/\Gamma\left( 1+1/\kappa\right) ^{2}-1\right] $](img174.gif) である.
である.
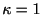 のときにワイブル分布は指数分布になる. 分布関数は
のときにワイブル分布は指数分布になる. 分布関数は
Figure 1.5:
ワイブル密度分布 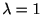 ,
,
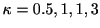
Figure 1.6:
ワイブル分布関数 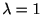 ,
,
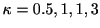
Figure 1.7:
ワイブル分布のハザード関数
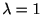 ,
,
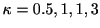
![\includegraphics[width=1\columnwidth]{graphics/book__4.eps}](img177.gif)
![\includegraphics[width=1\columnwidth]{graphics/book__5.eps}](img178.gif)
![\includegraphics[width=1\columnwidth]{graphics/book__6.eps}](img179.gif) |
逆ガウス分布
神経細胞スパイクの場合は, 死亡率と全く逆のハザード関数が描ける. 神経細胞のスパイク活動のISIを良く表すとされる逆ガウス分布(Inverse Gaussian distribution)[]を見てみよう.
逆ガウス分布の期待値は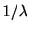 , 分散は
, 分散は
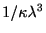 , また
, また
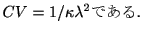 また累積分布関数は
逆ガウス分布のハザード関数を見てみると増加から減少に転じている. スパイク発生率はゼロから始まり, 時間とともに増加する.
これはガンマ分布のハザード関数と同じ性質である. ガンマ分布と違うのは,
ハザード関数が減少に転じる点にある.
つまり時間が経つにつれてスパイク発生頻度は減少していく.
また累積分布関数は
逆ガウス分布のハザード関数を見てみると増加から減少に転じている. スパイク発生率はゼロから始まり, 時間とともに増加する.
これはガンマ分布のハザード関数と同じ性質である. ガンマ分布と違うのは,
ハザード関数が減少に転じる点にある.
つまり時間が経つにつれてスパイク発生頻度は減少していく.
Figure 1.8:
逆ガウス密度分布 平均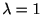 .
.
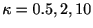
Figure 1.9:
逆ガウス分布のハザード関数 平均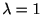 .
.
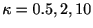
![\includegraphics[width=1\columnwidth]{graphics/book__7.eps}](img186.gif)
![\includegraphics[width=1\columnwidth]{graphics/book__8.eps}](img187.gif) |





Next: 定常スパイク時系列の実現
Up: 定常スパイク時系列モデル
Previous: 定常ポアソン過程
Contents
Index
© 2007 2008 2009 2010 H. Shimazaki, Ph.D.
![]() [ms]の間は次のスパイクを生成できない状態になる. これを絶対不応期(Absolute refractory period)と呼び, 神経細胞のリニューアル性の主要な要因である.
この他にも膜上の電位依存性イオンチャネルの非線形効果により, 一度スパイクが生じると複数回のスパイク生成が続くバースト発火という現象などがある. こうした性質を表現するためには, リニューアル過程の活用が欠かせない.
[ms]の間は次のスパイクを生成できない状態になる. これを絶対不応期(Absolute refractory period)と呼び, 神経細胞のリニューアル性の主要な要因である.
この他にも膜上の電位依存性イオンチャネルの非線形効果により, 一度スパイクが生じると複数回のスパイク生成が続くバースト発火という現象などがある. こうした性質を表現するためには, リニューアル過程の活用が欠かせない.
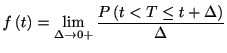
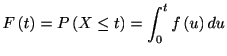
![]() 秒間スパイクが生成されず,
秒間スパイクが生成されず, ![]() においてスパイクを生成する確率として, 瞬間スパイク生成率
においてスパイクを生成する確率として, 瞬間スパイク生成率
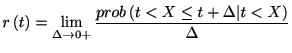
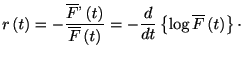
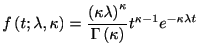
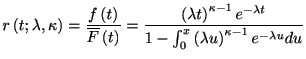
![$\displaystyle f\left( t;\lambda,\kappa\right) =\sqrt{\frac{\kappa}{2\pi t^{3}}}\exp\left[
-\frac{\kappa}{2t}\left( \lambda t-1\right) ^{2}\right]$](img180.gif) for
for
![$\displaystyle F\left( t;\lambda,\kappa\right) =\frac{1}{2}\left\{ 1+\operatorna...
...f}\left[ \sqrt
{\frac{\kappa}{2t}}\left( \lambda t+1\right) \right] \right\} .
$](img185.gif)