| HOME PAGE |
| Spike Density Estimation |
| - Histogram Method |
| - Kernel Method |
| Share it with your friend |
| Tweet |
本章では定常スパイク時系列を計算機上で実現するための数値計算法を紹介する. スパイク時系列の実現するためには, 特定の分布に従う確率変数を生成する必要がある. このとき様々な確率分布を一様分布に標準化して考えるのが基本になる. 同様に, リニューアル過程の瞬間スパイク生成率を規格化し, ポアソン過程に標準化して考えることもできる. この考え方は, 次節以降で非定常のスパイク時系列を実現する際に用いられる時間伸縮理論の基礎になる.
指数分布・ガンマ分布・ワイブル分布・逆ガウス分布等のスパイク密度分布に従う確率変数を生成したい. 特定の分布に従う確率変数を生成する方法に逆関数法がある. 逆関数法を理解するために,
次のような2つの確率変数の確率密度分布の関係を考えよう. 確率密度分布
![]() に従う確率変数(乱数)
に従う確率変数(乱数)![]() と,
と,
![]() と
と
![]() なる関係がある変数
なる関係がある変数![]() を考える.
を考える.
![]() が確率変数だから
が確率変数だから![]() も確率変数である.
このとき確率変数
も確率変数である.
このとき確率変数![]() の確率密度分布
の確率密度分布
![]() は
は
![]() を用いてどのように表現されるだろうか. 確率密度の保存則
を用いてどのように表現されるだろうか. 確率密度の保存則
![]() から
から![]() の確率密度分布
の確率密度分布
![]() は
は
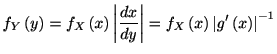
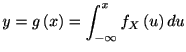
そこで逆に, ![]() を
を
![]() の区間の一様乱数として,
の区間の一様乱数として,
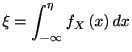
指数分布の場合は逆関数が解析的に求められる. 平均![]() の指数分布を考え
の指数分布を考え
![$\displaystyle \xi=\int_{0}^{\eta}\lambda e^{-\lambda x}dx=\left[ -e^{-\lambda x}\right]
_{0}^{\eta}=1-e^{-\lambda\eta}%
$](img210.gif)
| (1.19) |
ワイブル分布の分布関数から
![$\displaystyle \eta=-\frac{\left[ -\log\xi\right] ^{1/\kappa}}{\Gamma\left( 1+1/\kappa \right) \lambda}.$](img214.gif) |
(1.20) |
逆関数を解析的に求めることができないときにも, 所望の分布に従う確率変数を生成することができる. 一様乱数![]() を生成し, 数値積分により
を生成し, 数値積分により
![]() を満たす
を満たす![]() を求めればよい. ガンマ分布・逆ガウス分布に従う確率変数はこの方法で得ることができる.
を求めればよい. ガンマ分布・逆ガウス分布に従う確率変数はこの方法で得ることができる.
ハザード関数からスパイクを生成する場合, 分布関数とハザード関数の関係式に注目する.
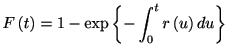
![$\displaystyle \int_{0}^{t}r\left( u\right) du=-\log\left[ 1-F\left( t\right) \right] .$](img219.gif) |
(1.21) |
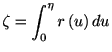
リニューアル過程ではスパイク間隔
![]() を独立に生成してよい.
を独立に生成してよい. ![]() 番目のスパイク時刻を
番目のスパイク時刻を
![]() として, スパイク時系列
として, スパイク時系列
![]() が得られる.
が得られる.
ただし初期スパイクのスパイク密度分布は平衡分布
| (1.22) |