| HOME PAGE |
| Spike Density Estimation |
| - Histogram Method |
| - Kernel Method |
| Share it with your friend |
| Tweet |
統計的推測の理論と実践はカール・ピアソン(Karl Pearson)とロナルド・エイルマー・フィッシャー(R.A. Fisher)によって築かれた. ピアソンはデータの背後に潜む統計モデルという概念を明確にし, 統計モデルの母数をデータから決定して科学的な検証に使うことを推進した. フィッシャーはデータから得られる統計量と統計モデルの母数とを明確に区別し,統計量(推定量)の望ましい性質を論じた.そして,繰り返し行われる実験によりデータを集めて, 統計モデルの母数を推定する最尤法を推進し統計的推測の理論を確立した. フィッシャーの打ち立てた統計的推測の理論の強力な仮定は, 母数が定数であることである. 計測期間中に母数が変動したり, 試行ごとに母数が変動することは想定しない. 神経科学における実験パラダイムも, これに従い同一実験下で 繰り返し実験を行うのが主流である. 現代はこのような制約から離れ,現実世界で得られるデータから統計的な判断を下す必要に迫られているために, ベイズ統計学が隆盛である.
![]() をパラメータ
をパラメータ![]() の推定量とする. 例をあげてみよう.
の推定量とする. 例をあげてみよう. ![]() が平均
が平均![]() の指数分布に従う乱数とすると,
の指数分布に従う乱数とすると, ![]() の推定量
の推定量
![]() の例としてまず考えられるのが, 平均
の例としてまず考えられるのが, 平均
![]() , がある. 推定量は他にも考えられる. 例えば初めのサンプルだけを使う
, がある. 推定量は他にも考えられる. 例えば初めのサンプルだけを使う
![]() も
も![]() の推定量である. では,
望ましい推定量とはどのような性質を持つべきだろうか.
平均二乗誤差はその一つの基準を与えると考えられる.
の推定量である. では,
望ましい推定量とはどのような性質を持つべきだろうか.
平均二乗誤差はその一つの基準を与えると考えられる.
| MSE | ||
| (4.2) |
ただし
![]() ,
,
![]() ,
,
![]() .
.
どれが一番小さいか.
| MSE |
||
| MSE |
||
| MSE |
尤度(likelihood)を最大にするパラメータを最尤推定量という.
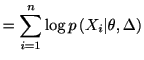 |
||
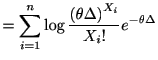 |
||
![$\displaystyle =\sum_{i=1}^{n}[X_{i}\log\left( \theta\Delta\right) -\theta\Delta-\log X_{i}!]$](img508.gif) |
![$\displaystyle =\sum_{i=1}^{n}[\frac{X_{i}%
}{\theta}-\Delta]$](img510.gif) |
||
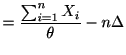 |
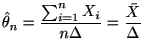
最尤推定値の期待値は
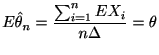
![$\displaystyle =E\left[ \frac{\sum_{i=1}%
^{n}X_{i}}{n\Delta}-\theta\right] ^{2}$](img517.gif) |
||
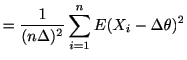 |
||
発火率![]() の定常ポアソン過程に従うスパイク時系列を得たとしよう. スパイク時系列をごく短い
の定常ポアソン過程に従うスパイク時系列を得たとしよう. スパイク時系列をごく短い![]() 秒の
秒の![]() 個のビンに区切り,
個のビンに区切り, ![]() 番目のビンにスパイクが存在すれば
番目のビンにスパイクが存在すれば![]() , しなければ
, しなければ![]() として,
として,
![]() をベルヌーイ過程と見なす.
このとき統計量
をベルヌーイ過程と見なす.
このとき統計量
![]() はベルヌーイ過程の
はベルヌーイ過程の![]() に関する十分統計量である.
に関する十分統計量である.
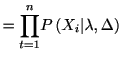 |
||
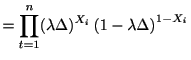 |
||
今度は定常ポアソン過程をやや大きめの![]() 個の観測区間
個の観測区間![]() で区切ったとしよう.
このとき各区間内のスパイクの個数
で区切ったとしよう.
このとき各区間内のスパイクの個数
![]() は平均
は平均
![]() のポアソン分布に従う. このとき
のポアソン分布に従う. このとき
![]() は
は![]() に関する十分統計量である.
に関する十分統計量である.
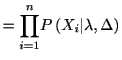 |
||
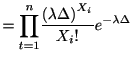 |
||
一般に密度分布のモデル
![]() が
が
| (4.3) |
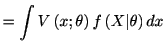 |
||
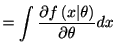 |
||
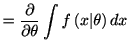 |
||
![$\displaystyle E[V^{2}]=E\left[ \frac{\partial}{\partial\theta}\log f\left( X\vert\theta
\right) \right] ^{2}%
$](img551.gif)
コーシー・シュワルツの不等式(Cauchy-Schwarz inequality)
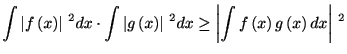 |
(4.5) |
![$\displaystyle E[V^{2}]\cdot E[(\hat{\theta}-\bar{\theta})^{2}]\geq\left\vert E\left[
V(\hat{\theta}-\bar{\theta})\right] \right\vert ^{2}%
$](img554.gif)
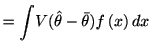 |
||
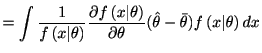 |
||
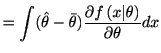 |
||
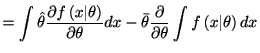 |
||
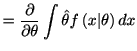 |
||
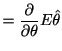 |
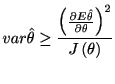 |
(4.6) |
| (4.7) |
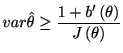 |
(4.8) |
フィッシャー情報量は次のようにも書ける.
![$\displaystyle J\left( \theta\right) =E\left[ \left( \frac{\partial}{\partial\th...
...rac{\partial^{2}%
}{\partial\theta^{2}}\log f\left( x\vert\theta\right) \right]$](img569.gif) |
(4.9) |
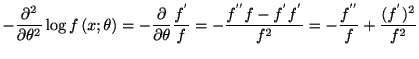
![$\displaystyle E\left[ -\frac{f^{^{\prime\prime}}}{f}+\left( \frac{f^{^{\prime}}...
...e}}}{f}\right]
^{2}=E\left[ \frac{\partial}{\partial\theta}\log f\right] ^{2}%
$](img571.gif)
ポアソン分布のフィッシャー情報量.
定常ポアソンスパイク時系列を![]() 個の観測区間
個の観測区間![]() で区切ったとしよう. このとき各区間内のスパイクの個数
で区切ったとしよう. このとき各区間内のスパイクの個数
![]() は平均
は平均
![]() のポアソン分布
のポアソン分布
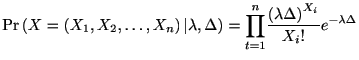
![$\displaystyle =-E\left[ \frac{\partial^{2}}{\partial \lambda^{2}}\log f\left( X;\lambda,\Delta\right) \right]$](img575.gif) |
||
![$\displaystyle =-E\left[ \frac{\partial^{2}}{\partial\lambda^{2}}\sum_{i=1}^{n}\left( X_{i}\log\lambda\Delta-\lambda\Delta-\log X_{i}!\right) \right]$](img576.gif) |
||
![$\displaystyle =-E\left[ \sum_{i=1}^{n}\frac{\partial}{\partial\lambda}\left( X_{i}%
\frac{1}{\lambda}-\Delta\right) \right]$](img577.gif) |
||
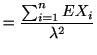 |
||
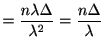 |
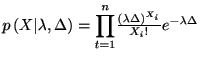 の
の
指数分布のフィッシャー情報量を求めよ![]()
![$\displaystyle J\left( \lambda\right) =-E\left[ \frac{\partial^{2}}{\partial\lam...
...tial\lambda}\left( \frac{1}{\lambda}-x\right) \right] =\frac
{1}{\lambda^{2}}%
$](img585.gif)
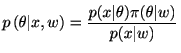
分母は正規化項で分子の総和をとって
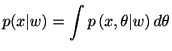
事後損失関数(posterior loss function, posterior expected loss) を定義し,事後分布による期待値: 事後リスク関数(posterior risk function)
![$\displaystyle L^{\text{Bayes}}(\delta,\theta;X,w)\equiv E^{\theta\vert X,w}[L(\...
...eta)]=\int L\left( \delta,\theta\right) p\left( \theta\vert X,w\right)
d\theta
$](img592.gif)
損失関数として支持関数(indicator function)![]()
損失関数として絶対誤差![]()
損失関数として二乗誤差![]()
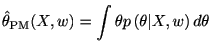
ベイズ推定量は超パラメータに依存する.超パラメータを最尤推定で求めベイズ推定量に用いることを経験ベイズ法と呼ぶ(empirical Bayes estimator).