HOME PAGE

Spike Density Estimation

- Histogram Method

- Kernel Method

Share it with your friend

Tweet

非定常リニューアル過程

変動レートの時間伸縮

非定常リニューアル過程は変動ポアソン過程の場合を拡張して考えるとわかりやすい. 非定常ポアソン過程と同様に時間伸縮した軸上で定常リニューアル過程を考える. 例として$\Lambda$上の定常ガンマ過程を考え, そのイベント系列を $\left\{ \Lambda_{1},\Lambda_{2}% ,\cdots\right\}$とする. イベント間隔 $\Lambda_{i}-\Lambda_{i-1}$が平均が$1$, 分散が$1/\kappa$である標準ガンマ分布

$$g\left( z;\kappa\right) =\frac{1}{\Gamma\left( \kappa\right) }% \kappa\left( \kappa z\right) ^{\kappa-1}e^{-\kappa z}%$$

に従うとする[Berman, 1981,Barbieri et al., 2001]. $\kappa$はshape parameterと呼ばれる. 実時間との対応は $\Lambda_{i}=\Lambda\left( t_{i}\right)$だから, ガンマ分布に従う乱数を発生させ, 変数変換の公式

$$z\left( t_{i}\vert t_{i-1},\lambda_{t_{i-1}:t_{i}}\right) =\Lambd... ...Lambda\left( t_{i-1}\right) =\int_{t_{i-1}}^{t_{i}}% \lambda\left( u\right) du$$

を満たす$t_{i}$を逐次的に求めれば, 実時間でのスパイク時系列を求めることができる.

条件付きスパイク密度分布

ガンマ分布

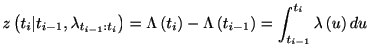
条件付きスパイク密度分布 $p\left( t_{i}\vert t_{i-1},\left\{ \lambda _{t}\right\} \right)$を求めよう. 分布 $p\left( t_{i}\vert t_{i-1},\left\{ \lambda _{t}\right\} \right)$は次のような$t_{i}$から$z$への変数変換（タイムリスケーリング）を施すことで, 標準ガンマ分布になるとする. すなわち, 変数変換の公式から

$$g\left( z\vert t_{i-1},\lambda_{t_{i-1}:t_{i}}\right) =\left\vert... ...{dt}\right\vert ^{-1}p\left( t_{i}\vert t_{i-1},\lambda_{t_{i-1}:t_{i}}\right)$$

$dz/dt_{i}=\lambda\left( t_{i}\right)$に注意して

$$p\left( t_{i}\vert t_{i-1},\lambda_{t_{i-1}:t_{i}}\right) =\left\vert \frac{dz}{dt_{i}}\right\vert g\left( z\vert t_{i-1},\lambda_{t_{i-1}:t_{i}}\right)$$

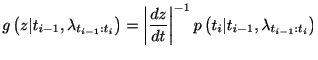
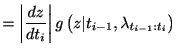$$=\lambda\left( t_{i}\right) \frac{1}{\Gamma\left( \kappa\right) }... ...appa-1}\exp\left[ -\kappa\int_{t_{i-1}}^{t_{i}}\lambda\left( u\right) du\right]$$

となる.

ワイブル分布

平均$1$・分散 $\Gamma\left( 1+2/\kappa\right) /\Gamma\left( 1+1/\kappa\right) ^{2}-1$の標準ワイブル分布は

$$g\left( z;\kappa\right) =\kappa\Gamma\left( 1+1/\kappa\right) \le... ...}\exp\left[ -\left\{ \Gamma\left( 1+1/\kappa\right) t\right\} ^{\kappa}\right]$$

$dz/dt_{i}=\lambda\left( t_{i}\right)$に注意して

$$p\left( t_{i}\vert t_{i-1},\lambda_{t_{i-1}:t_{i}}\right) =\left\vert \frac{dz}{dt_{i}}\right\vert g\left( z\vert t_{i-1},\lambda_{t_{i-1}:t_{i}}\right)$$

$$=\lambda\left( t_{i}\right) \kappa\Gamma\left( 1+1/\kappa\right) ... ...appa\right) \int_{t_{i-1}}^{t_{i}}\lambda\left( u\right) du\right\} ^{\kappa-1}$$

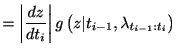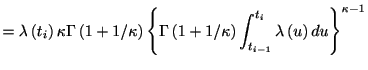$$\cdot\exp\left[ -\left\{ \Gamma\left( 1+1/\kappa\right) \int_{t_{i-1}% }^{t_{i}}\lambda\left( u\right) du\right\} ^{\kappa}\right]$$

となる.

逆ガウス分布

同様にして, 逆ガウス分布に従うリニューアル過程は, 平均$1$・分散$1/\kappa$の標準逆ガウス分布

$$g\left( z;\kappa\right) =\sqrt{\frac{\kappa}{2\pi z^{3}}}\exp\left[ -\frac{\kappa}{2z}\left( z-1\right) ^{2}\right]$$

を用いてISI分布は

$$p\left( t_{i}\vert t_{i-1},\lambda_{t_{i-1}:t_{i}}\right) =\left\vert \frac{dz}{dt_{i}}\right\vert g\left( z\vert t_{i-1},\lambda_{t_{i-1}:t_{i}}\right)$$

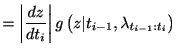$$=\lambda\left( t_{i}\right) \sqrt{\frac{\kappa}{2\pi\left\{ \int_... ...ght) du-1\right\} ^{2}}{\int_{t_{i-1}}^{t_{i}}\lambda\left( u\right) du}\right]$$

となる.

時間伸縮理論

条件付きスパイク密度分布が求まれば, これから瞬間スパイク生成率(ハザード関数)が求まる.

$$r\left( t_{i}\vert t_{i-1},\lambda_{t_{i-1}:t_{i}}\right) =\frac{... ..._{t_{i-1}}^{t_{i}% }p\left( u\vert t_{i-1},\lambda_{t_{i-1}:t_{i}}\right) du}%$$

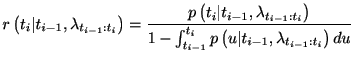
瞬間スパイク生成率が求まれば, 時間を十分小さな幅$\Delta$のビンに区切って確率 $r\left( t_{i}\vert t_{i-1},\lambda_{t_{i-1}:t_{i}}\right) \Delta$でスパイクを発生させればよい. もちろんこの方法は効率が悪い.

瞬間性スパイク生成率 $r\left( t_{i}\vert t_{i-1},\lambda_{t_{i-1}:t_{i}}\right)$が求まれば, 非定常リニューアル過程であっても非定常ポアソン過程としてあつかえる. 非定常ポアソン過程の時と同様に $r\left( t_{i}\vert t_{i-1},\lambda_{t_{i-1}:t_{i}}\right) \Delta$を積分すると

$$\zeta=\int_{t_{i-1}}^{t_{i}}r\left( u\vert t_{i-1},\lambda_{t_{i-1}:t_{i}}\right) du$$

$t_{i}$が $p\left( t_{i}\vert t_{i-1},\lambda_{t_{i-1}:t_{i}}\right)$に従うとき, $\zeta$は指数分布に従う. したがって指数分布に従う乱数 $\zeta$を生成し, 数値計算で上式を満たす$t_{i}$を求めればよい. 時間伸縮理論を用いたこの方法は非常に汎用性のある方法で, より一般の点過程について成り立つから証明はそこで示そう. ここでは, この時間伸縮理論に基づいた数値計算アルゴリズムをまとめておく.

アルゴリズム 12   時間伸縮理論を用いた非定常リニューアル過程の実現

1. $i=1,t_{1}=0.$

2. レート$1$の指数分布に従う乱数$\eta$を生成する.

3. 時間伸縮 $\Lambda_{t}=\int_{0}^{t}\lambda\left( u\right) du$により, 伸縮したISIを求める. $z_{t}=\Lambda_{t}-\Lambda_{t_{i-1}}$

4. ISI分布を求める $p\left( t\vert t_{i-1},\lambda_{t_{i-1}:t_{i}}\right) =\lambda\left( t\right) g\left( z_{t}\vert t_{i-1},\lambda_{t_{i-1}:t_{i}}\right)$

5. ハザード関数を求める

6. $r\left( t\vert t_{i-1},\lambda_{t_{i-1}:t}\right) =\frac{p\left( t\vert t_{i-1... ...ht) }{1-\int_{t_{i-1}}^{t}p\left( u\vert t_{i-1},\lambda_{t_{i-1}:u}\right) du}$

7. $\eta=\int_{t_{i-1}}^{t}r\left( u\vert t_{i-1}\right) du$を満たす$t_{i}$を求める.

8. $t_{i}\geq T$ならば終了.

9. $t_{i}<T$ならば $i\leftarrow i+1.\ 2$へ.

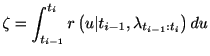
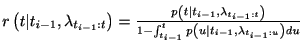
このアルゴリズムによる数値シミュレーションの結果を示す.

Figure 2.2: 時間依存する強度に従うポワソン及びリニューアル過程. 青色の点線が時間依存する変動スパイクレート. 赤色の実線はスパイク発火を考慮した強度関数. (A) 非一様ポワソン過程 (B) 非一様逆ガウス過程 (C) 非一様ガンマ過程 （規則発火 κ=1.8) (D) 非一様ガンマ過程 （不規則発火 κ=0.8）

使用したMatlabのコード. 数値積分は台形則を用いている.

function [x,rs] = PointProcess_Renewal(y,dt,ISI,k)
% [x,rs] = PointProcess_Renewal(y,dt,ISI,k)
% Function `PointProcess_Renewal' returns sample spike events
% from a time-dependent Renewal point process.
% 
% Example usage:
% dt = 0.001; t = [0: dt: 1];   % Time resoluation and time-axis.
% y = 10*(1+cos(2*pi*1*t));     % Time-dependent spike-rate.
% k = 2.3;                      % Shape parameter. 
% x = PointProcess_Renewal(y,dt,'Gamma',k)
% 
% Input argument
% y:    A vector that specifies a time-dependent spike-rate.
% dt:   Sampling time of the time-dependent rate.
% ISI:  Type of Inter-spike Interval (ISI) distribution.
%       'Gamma', Gamma distribution.
%       'InvGauss', Inverse Gamma distribution.
%       'Weibull', Weibull distribution.
% k:    The shape parameter of the ISI distribution.
%       * To use small k << 1, use small sampling time dt. 
%       * Maximum k allowed is ~10. 
%
% Output argument
% x:    Spike time.
% rs:   Intensity function.
%
% See also RASTER STOCHPROCES_GAUSS
%
% Copyright (c) 2007, Hideaki Shimazaki All rights reserved.
% http://2000.jukuin.keio.ac.jp/shimazaki

%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
%Initialize parameters
global invGammak;
invGammak = 1/gamma(k);

L = length(y);
x = zeros(1,round(mean(y)*L*dt + sqrt(mean(y)*L*dt)*3) );
rs = zeros(1,L); 

z = 0; P = 0; R = 0; j = 1; c = 1;

yb = y(1);
pb = y(1) * feval(ISI,0,k);
pb2 = pb;
rb = 0;

rs(1) = pb;

eta = - log(rand);
for i = 2: L
    %if eta > R 
        z = z + (yb+y(i))/2*dt;         %Time-rescale
        yb = y(i);

        p = y(i) * feval(ISI,z,k);      %ISI

        %P = P + (pb+p)/2*dt;
        if c == 1 
            P = p*dt;
        elseif c == 2
            P = (3/2*pb-1/2*p)*dt;                      %Semi-open
            P = P + (1/2*pb+1/2*p)*dt;                  %Trapezoidal
        elseif c == 3
            P = (23/12*pb2-16/12*pb+5/12*p)*dt;
            P = P + (1/3*pb2+4/3*pb+1/3*p)*dt;          %Simpson
        elseif c == 4
            P = (55/24*pb3-59/24*pb2+37/24*pb-9/24*p)*dt;
            P = P + (3/8*pb3+9/8*pb2+9/8*pb+3/8*p)*dt;  %Simpson 3/8
        else 
            P = P + (1/2*pb+1/2*p)*dt;
        end
        pb3 = pb2; pb2 = pb; pb = p;

        r = p / (1 - P);                %Intensity
        R = R + (rb+r)/2*dt;
        rb = r;
        
    if eta > R 
        c = c + 1;
        
    else
        x(j) = i*dt; j = j + 1;         %Spike time
        
        z = 0; P = 0; R = 0; c = 1;           

        yb = y(i);
        %pb = y(i) * feval(ISI,0,k);
        rb = 0;
        
        eta = - log(rand);
    end
    rs(i) = r;
end

x = x(x~=0);

if length(x) < sum(y*dt) - 3*sqrt(sum(y*dt))
    disp('Warning. Better to increase sampling resolution'); 
end


%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
% Inter-spike Interval distributions

function y = Gamma(z,k)
global invGammak

if k == 1
    y = exp(-z);
elseif z == 0 && k < 1
    y = 0;
else
    %y = 1/gamma(k) * k * (k * z).^(k-1) .* exp(-k*z);
    y = invGammak * k * (k * z).^(k-1) .* exp(-k*z);
end 

function y = InvGauss(z,k)
if z == 0
    y = 0;
else 
    y = sqrt( k/ (2*pi*z.^3) ) * exp( -k/2/z * (z-1)^2 ); 
end

function y = Weibull(z,k)
if z == 0 && k < 1
    y = 0;
else
    y = k*gamma(1+1/k)*(gamma(1+1/k)*z)^(k-1) * exp(-(gamma(1+1/k)*z)^k);
end

初期スパイクの生成について

リスケールした時間軸上で平衡リニューアル過程を考えればよいだろう. リスケールした軸上で初期スパイクのスパイク密度分布は

$$g_{1}\left( z\right) =1-G\left( z\right)$$

で与えられる. 実時間の初期スパイクのスパイク密度分布 $p_{1}\left( t\right)$は, 実時間上への逆写像を用いる.